Il numero $i$ come vedremo ci riserverà di molte sorprese! La prima delle quali è la sua ciclicità e lo stretto legame con le rotazioni nel piano di Gauss. Quando proviamo ad elevare $i$ ad una potenza, ciò che accade è un fatto assai particolare: si ottengono dei valori che via via, dopo un po si ripetono $$i^1 = i$$ $$i^2 = -1$$ $$i^3 = ii^2 = -i$$ $$i^4 = i^2i^2 = (-1)(-1) = 1$$ $$i^5 = ii^4 = i^2i^3 = i$$ $$i^6 = -1$$ $$...$$ Come vedete si ha una successione di simboli che si ripetono dopo ogni $4^a$ potenza. Riportiamo alcuni termini della successione: Se ci mettiamo nel piano complesso, possiamo dare una immediata e potente "interpretazione geometrica" della potenza di $i$. Infatti nel piano complesso i termini della successione delle potenze immaginarie occupano dei punti particolari sul cerchio unitario, questi punti coincidono con gli assi reale ed immaginario come meglio evidenziato in figura.

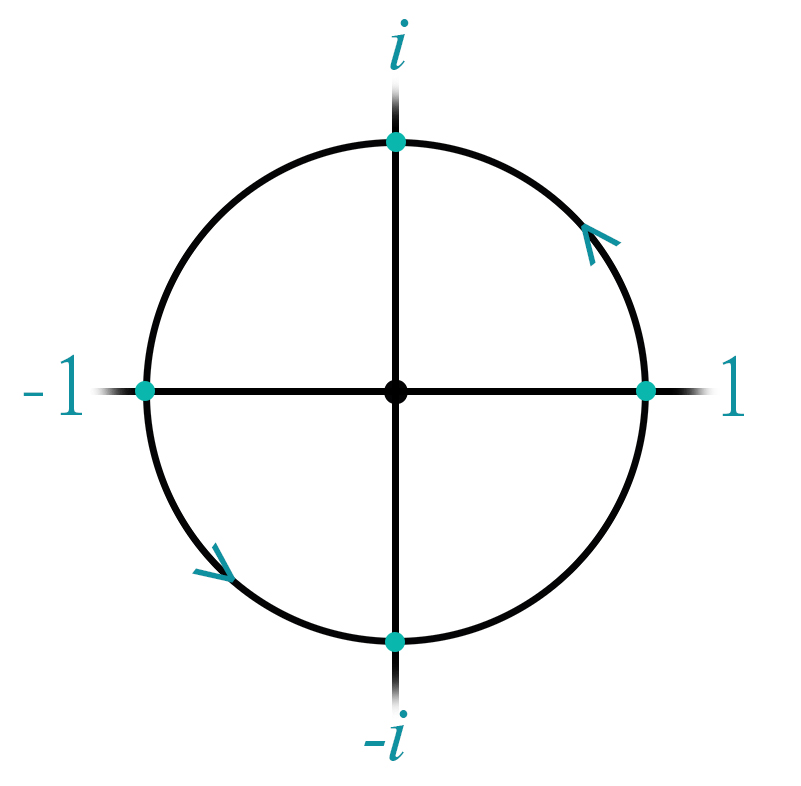
Se ora ricordiamo la regola del prodotto di due numeri complessi e la specifichiamo al caso particolare di prodotto per $i$ ci accorgiamo che l'effetto sul piano complesso è quello di una rotazione antioraria di $90°$ o $\frac{\pi}{2}$ radianti; mentre il raggio resta invariato (dal momento che il modulo di $i$ è sempre unitario). Quindi quando facciamo delle potenze di $i$ in realtà stiamo ruotando in senso antiiorario sul cerchio unitario di angoli di $90°$ per volta.

Per calcolare ad esempio $i^3$ ci posizioniamo sul punto $(1, 0)$ a destra (che corrisponde a $i^0=1$ "nessuna rotazione") ed operiamo una rotazione di $90°*3 = 270°$ (ciò equivale a 3 volte il prodotto di $i$ per se stesso). Se volessimo calcolare ora ad esempio: $${\large i^{20}}$$ E' semplice! Basta ricordarsi che $i^4$ equivale ad un giro completo quindi dobbiamo fare in tutto $20 / 4 = 5$ rotazioni, ottenendo come risultato $1$ quindi: $i^{20} = 1$. Naturalmente bisogna tenere conto dell'angolo percorso che vale $5*360° = 1800°$ o $10\pi$ radianti.