Immaginate cosa accadrebbe se viaggiassimo "a cavallo di un raggio di luce!" Materia strana la luce... Eppure c'è chi è riuscito a carpirne i più profondi misteri e a svelarne le più spettacolati caratteristiche. Albert Einstein, forse lo scienziato più famoso al mondo nella sua Teoria della relatività, ci ha aperto la strada ad un viaggio senza fine, che ancor oggi prosegue, inarrestabile verso la scoperta delle meraviglie dell'universo. In questa chiacchierata vedremo brevemente, anzi direi, sommariamente un assaggio di una sezione dedicata all'argomento Einstein che io ed il collega e amico Loris Fato stiamo preparando per voi. Questa sezione, vi anticipo sarà un viaggio nel mondo di Einstein, nella sua vita, nell'universo, nelle scoperte e soprattutto nella sua creatura, la più bella delle teorie: la Teoria della Relatività. Questo non vuole essere un articolo tecnico, ma solo una lettura di riscaldamento per il futuro, perlomeno nel momento in cui sto scrivendo questa pagina... ma iniziamo con i prerequisiti, ossia, la relatività galileiana e l'elettromagnetismo...
$$ \diamond $$
Il gran naviglio di Galileo
Immaginiamo di essere nella stanza di una nave, in compagnia di un nostro amico. La nave ad esempio, un grosso vascello, si muove solo in avanti, senza la minima vibrazione o rotazione laterale. Naturalmente voi sapete di essere in una nave, ma fate finta di essere ad esempio, in un laboratorio. In questo laboratorio, tutte le porte e le finestre sono chiuse, di modo che non riuscite a vedere all'esterno, cosa sta succedendo... Avete a disposizione, solo degli oggetti con cui fare esperimenti ed osservare dei fenomeni meccanici . Bella cosa, direte, specilmente se siete dei fisici! Osservate la bottiglia che gocciola dell'acqua in un vaso dal collo molto stretto, provate a saltare a piedi uniti in tutte le direzioni, inoltre lanciate una palla al vostro amico e viceversa, fatevela lanciare - (non fatevi colpire in faccia :-) . Guardate le mosche in aria che svolazzano di quà e la da ogni dove... Ebbene, tutti questi esperimenti fatti in un laboratorio fermo "a terra" sono assolutamente leciti, ma non vi scordate che siete in una nave, e che naturalmente la nave puo muoversi. Ora la domanda è: se la nave si muove di moto rettilineo uniforme, (senza vibrazioni varie, frenature, accelerazioni ecc...) questi esperimenti cambiano? ad esempio la goccia potreste pensare che nel momento in cui sta cadendo, siccome la nave sta avanzando esce dal vaso (perchè il vaso si è spostato in avanti mentre la goccia era per aria) - oppure, la palla che lanciate al vostro amico risente della velocità della nave? E così via. Ebbene, il principio di relatività galileiana afferma che non c'è alcuna distinzione! Non potete scoprirlo. Con nessun esperimento si può distinguere se un sistema e fermo o è in moto rettilineo uniforme!

Trasformazioni di Galileo
Le trasformazioni di Galileo esprimono quanto detto in termini matematici. Se consideriamo due sistemi di riferimento inerziali, ossia per cuio le leggi della fisica sono le più semplici possibile, in cui vale il principio d'inerzia \( Oxyz \) ed \( O'x'y'z' \) possiamo mostrare come il tutto sia in accordo con quanto appena detto. Supponendo che i sistemi abbiano la stessa orientazione e che gli assi \( x\) ed \( x'\) siano sovrapposti ed inoltre che all'istante \( t = 0\) le origini coincidano \(O = O'\) e che la velocita del sistema mobile rispetto al sistema fisso sia \( \vec{v} \) avremo che:
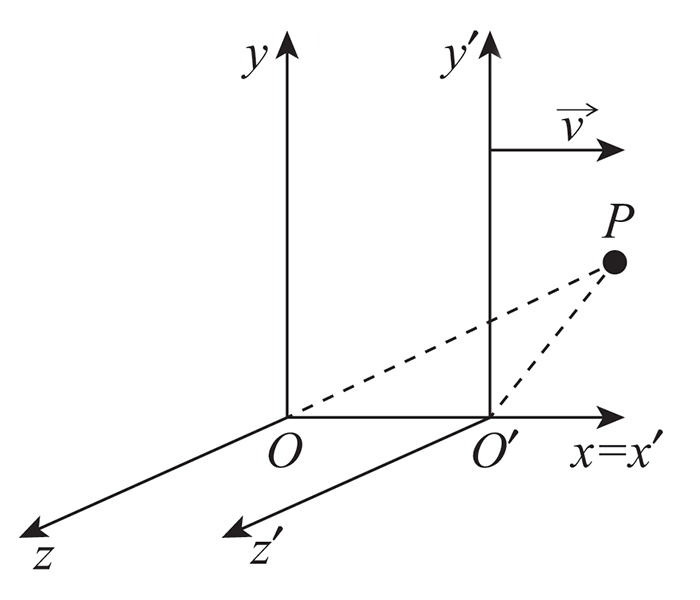
Questo mostra che le leggi della meccanica sono covarianti, nel senso che sono invarianti per trasformazioni di galileo, quando si passa da un sistema inerziale ad un altro che si muove rispetto al primo a velocità costante. Vi faccio notare che il tempo naturalmente, come suggeritoci dal grande Newton è assoluto. Ma ora passiamo all'altro caposaldo della fisica, l'elettromagnetismo
$$ \diamond $$La grande sintesi di Maxwell
Quando si parla di unificazione, non si può non parlare di elettromagnetismo, di Maxwell, di campi ed onde... di quel regno straordinario dove la fisica, come direbbe qualcuno è "metafisica" e la matematica descrive onde corpuscoli, interferenze, campi ed altri fenomeni straordinari. Einstein partì da un'incongruenza o come diceva lui, una asimmetria tra le leggi della meccanica di galileo e l'elettromagnetismo, e definì il suo principio di relatività ristretta che sulla base di alcuni postulati che hanno portato poiall'estensione dell'invarianza delle leggi fisiche anche per l'elettromagntismo, che era escluso dai principi galileiani. Ma di questo ne parleremo successivamente. Il cuore della teoria si riassume in sole 4 equazioni! Le cosiddette Equazioni di Maxwell, che riassumono tutti i fenomeni elettromagnetici con una manciata di pochi simboli matematici... Iniziamo il nostro viaggio facendo conoscenza con esse e cerchiamo di spiegarne perlomeno il significato da un punto di vista "ad alto livello", poi, per i più volentersi, vi anticipo che sto preparando un minicorso, dove ciascuna di esse sarà approfondita nei minimi dettagli". Le equazioni si presentano in vari modi; nella forma, cosiddetta "differenziale" esse sono:

Anzitutto, notate che in ogni equazione compare il simbolo \( \nabla \). Si tratta di un oggetto speciale, che i fisichi chiamano \( nabla \). E' sostanzialmente un operatore che opera nello spazio e generalizza il concetto di derivata a più dimensioni. In esso sono racchiusi tutti i procedimenti differenziali di approssimazione locale, e per questo molto spesso le equazioni in cui compare nabla vengono dette equazioni in forma locale. Ad esempio in \( \mathbb R^3\), assume la forma seguente:
- \( \bullet \) La prima equazione esprime il Teorema di Gauss per il campo elettrico. Sostanzialmente ci informa che il campo elettrico è generato dalle cariche elettriche disposte in una regione dello spazio. Il termine a sinistra \( \nabla \cdot \mathrm E\) si chiama divergenza di \( \mathrm E\) che tradizionalmente si indica: \( \mathrm{divE} \). La divergenza di un campo, è un valore che esprime localmente come il campo diverge o converge in un punto. Il fatto che ci sia una divergenza del campo elettrico, significa che esistono, da qualche parte nello spazio, punti dalla quale si genera il campo - questi punti, come è espresso nel membro di destra dell'equazione, sono le cariche elettriche (a meno della costante \( \epsilon_0\) che descrive le proprietà del mezzo), che nel caso esse sono positive, sono sorgenti del campo, nel caso esse sono negative, sono dei pozzi dove il campo confluisce.
- \( \bullet \) Per quanto riguarda la seconda equazione, si tratta della versione del Teorema di Gauss per il campo magnetico, che è \(0\). La divergenza nulla, indica che il campo magnetico non nasce e non confluisce in nessun punto! Una strana proprietà che implica la non esistenza di "cariche magnetiche" e che nel linguaggio dei fisici si chiama solenoidalità. Un campo solenoidale non ha ne sorgenti, ne pozzi.
- \( \bullet \) La terza equazione e la Legge di Faraday-Neumann-Lenz della Induzione Elettromagnetica. In questa e nella quarta equazione compare a primo membro un aggeggio chiamato rotore che descrive in un modo molto suggestivo, i vortici di un campo; ossia se il campo ruota localmente, intorno ad un asse o un punto. L'uguaglianza è tra il rotore del campo elettrico, e la variazione temporale di campo magnetico. Più semplicemente se c'è un campo magnetico variabile nel tempo, si genera un campo elettrico.
- \( \bullet \) L'ultima equazione è la Legge di Ampére-Maxwell, che ci dice una cosa assolutamente inaspettata: i campi magnetici sono generati dalle correnti elettriche, e, in aggiunta, dice Maxwell dalle correnti di spostamento.
Queste bellissime equazioni, come previsto dallo stesso Maxwell e dimostrato in seguito da Hertz, esprimono il campo elettromagnetico, ossia il modo in cui elettricità e magnetismo sono interconnesse l'una con l'altra in unico fenomeno fisico inscindibile! Da queste equazioni discende la formula per la velocità della luce, in seguito studiata da Einstein e da Michelson & Morley, nel loro esperimento del 1887.
Relatività Ristretta
Questa era l'aria che respirava Einstein, nel 1905 a Berna. Occupava il posto di impiegato all'ufficio brevetti ed era addetto all'analisi di approvazione di congegni meccanici ed elettronici vari... molte volte nei ritagli di tempo lavorava ai suoi articoli, scientifici, ai suoi studi sulla natura della luce. Un giorno lesse di un problema che lo colpì particolarmente. Il problema era legato alla sincronizzazione degli orologi. Dalla sua finestra si intravedeva la grande stazione ferroviaria di berna con i treni che partivano e giungevano dai binari e lui viaggiava con la mente e immaginava situazioni critiche in cui le leggi fisiche venivano sottoposte a dura prova. Presto capì che il problema non era banale, ma era legato alla natura intrinseca del tempo e dello spazio. Bisognava cambiare le leggi della fisica.
Simultaneità, Treni e fulmini
Einstein, partì da un esperimento mentale. Era tipico per Einstein, fare esperimenti mentali. L'esperimento è il seguente. Fingete di essere per un momento Einstein ed immaginate di essere in una stazione ferroviaria, magari a Berna, con il vostro migliore amico/a. Tu sei seduto sulla banchina ed ad un certo istante due fulmini (si fa per dire...) colpiscono due punti \( \mathrm A\) e \( \mathrm B\) equidistanti dalla tua posizione. Per te che stai seduto e fermo sulla banchina, i due fulmini sono eventi simultanei, infatti nell'istante \( t\), vedi i due fulmini generarsi "simultaneamente", perchè la luce viaggia a velocità finita e quindi impiega lo stesso tempo per giungere ai tuoi occhi; e credo tu sia in accordo con quanto detto!.
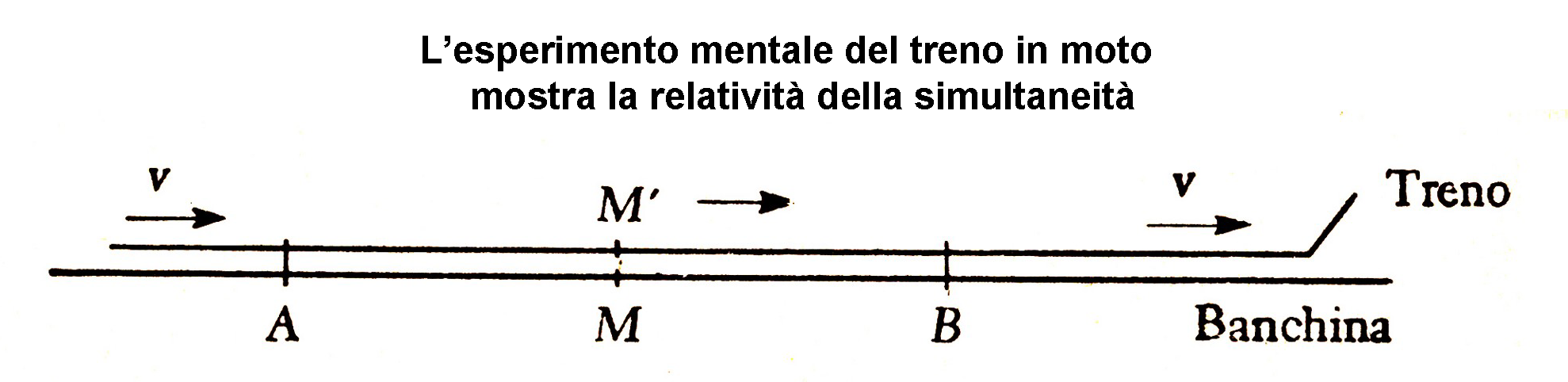
Ma ora arriva il bello... Immaginiamo, che il tuo amico si trovi in un treno. Il treno viaggia a velocità costante \( v\) rispetto a te che sei fermo. Il tuo amico sta guardando dal finestrino all'esterno, entrambi siete in ansia di ciò che sta per accadere... ad un certo istante nuovamente, i due fulmini si ripresentano nei medesimi punti \( \mathrm A\) e \( \mathrm B\). Ora; per te nulla è cambiato. Ma cosa ha visto il tuo caro amico dal treno in corsa? Una cosa sconvolgente! E cioè, per lui i due fulmini non sono giunti nello stesso istante nei due punti \( \mathrm A\) e \( \mathrm B\), per il semplice fatto che il treno sta avanzando e perciò lui vedra per primo il fulmine cui il treno si sta avvicinando che l'altro (cui si sta allontanando); dalla figura vedrà per primo \( \mathrm B\). Morale: ciò che è simultaneo per me che sono seduto, non è simultaneo per lui che è in movimento. Questà si chiama la relatività della simultaneità e rappresenta il punto di partenza di tutta la teoria.
Metrica eucludea vs metrica di Minkowsky: Lo SpazioTempo
La relatività ristretta (RR), è definita in uno spazio a quattro dimensioni. Spazio e tempo non sono più separati, ma costituiscono un tuttuno: lo spaziotempo. Ricordo che la metrica euclidea si ottiene sostanzialmente attraverso la norma della differenza tra due vettori, e la norma attraverso il prodotto scalare. Per quanto riguarda lo spaziotempo, i vettori spaziotemporali, si chiamano eventi e la metrica è una pseudo-metrica per via dei segni meno (-).
Metrica Euclidea
$$ \Delta_s^2 = c^2\Delta t^2-\Delta_x^2-\Delta_y^2-\Delta_z^2 $$
Metrica di Minkowski
Le Trasformazioni di Lorentz
Consideriamo due sistemi di riferimento inerziali, di moto traslatorio rettilineo ed uniforme l'uno rispetto all'altro. Il primo \( Oxyz\) fisso, il secondo \( O'x'y'z'\) mobile. Prendiamo due eventi \( (x, y, z, t) \) ed \( (x', y', z', t') \), nel primo e nel secondo sistema rispettivamente. Per quanto espresso dal principio di relatività, le leggi della fisica devono conservare la distanza, cambiando sistema di riferimento. Se ad esempio guardo un oggetto e mi sposto e lo guardo spostandomi un pò, ci siete che la lunghezza dell'oggetto non cambia? Ebbene le trasformazioni devono rispettare allora questa invarianza:
Gli effetti relativistici
Chiudiamo la nostra discussione con alcuni effetti relativistici, percepibili solo quando si viaggia a velocità prossime a quelle della luce! Gli effetti sono: La Dilatazione dei Tempi, la Contrazione delle lunghezze e l' Aumento della massa, le cui formule sono riportate di seguito:
Osservate che nelle formule compare il termine \({ 1 \over \sqrt{1-{v^2 \over c^2 }} }\). Si tratta di un'espressione che compare in molte relazioni relativistiche, include le trasformazioni di Lorentz. Per questo motivo gli si è dato un nome: il fattore relativistico. Tradizionalmente lo ritrovate indicato nei testi di relatività, con la lettera \( \gamma\). Il rapporto \( {v\over c} \) si indica invece con la lettera \( \beta\), per cui sostituendo: avremo che $$ \gamma = { 1 \over \sqrt{1-{v^2 \over c^2 }} } = { 1 \over \sqrt{1-{\beta^2}} } $$ E' facile dimostrare, e lo faremo, che le trasformazioni di Lorentz, nel caso di basse velocità rispetto a quelle della luce, diventano le Trasformazioni di Galileo, infatti il termine \( \beta = {v \over c} \rightarrow 0 \) per cui \(\gamma = \), il che dimostra la validità e la consistenza, perlomeno delle relazioni algebriche della teoria.
$$ \heartsuit $$\( \langle \) Il punto di arrivo del nostro viaggio per ora è arrivato, abbiamo scalfito un po di relatività ristretta, ci sarebbe da discutere anche di relatività generale, preparatevi a salire sul prossimo treno... \( \rangle \)


