Quando applichiamo l'operatore \( \nabla \) (del) ad un campo scalare, cioè ad una funzione \( F: {\mathbb R}^n \rightarrow {\mathbb R} \), otteniamo un oggetto speciale chiamato campo gradiente o semplicemente gradiente. Consideriamo ad esempio il campo scalare che descrive la temperatura in una stanza \( \Phi: {\mathbb R}^3 \rightarrow {\mathbb R} \). Esso associa ad ogni punto dello spazio \( {\mathbb R}^3 \) un valore numerico che rappresenta il valore della temperatura in quel punto. L'immagine del campo la possiamo indicare come: \( \Phi({\mathbb R}^3) \)
Applichiamo nabla a \( \Phi \): diamo, cioè, in input a: \( \nabla(\cdot) \) l'immagine di \( \Phi \) e vediamo cosa succede. Anzitutto l'operazione è lecita, in quanto nabla prende in input solo campi scalari; ma vediamo cosa otteniamo in output.
$${\large \color{#333333}{\nabla(\Phi) = \frac{\partial(\Phi)}{\partial x}\hat{i} + \frac{\partial(\Phi)}{\partial y}\hat{j} + \frac{\partial(\Phi)}{\partial z}\hat{k} }} $$ $${\large \color{#333333}{\nabla(\Phi) = \frac{\partial(\Phi)}{\partial x}\hat{i} + \frac{\partial(\Phi)}{\partial y}\hat{j} + \frac{\partial(\Phi)}{\partial z}\hat{k} }} $$ $${\large \color{#333333}{\nabla(\Phi) }} $$ $$ \downarrow $$ $${\large \frac{\partial(\Phi)}{\partial x}\hat{i} + \frac{\partial(\Phi)}{\partial y}\hat{j} + \frac{\partial(\Phi)}{\partial z}\hat{k} } $$Otteniamo un vettore! Questo vettore, ha per componenti le derivate parziali di \( \Phi \) lungo le tre direzioni canoniche \( \hat{i}, \hat{j}, \hat{k}, \). Queste componenti sono funzioni spaziali di \( x, y, x \), di conseguenza il vettore è un campo vettoriale che varia nello spazio; in tutto il dominio di \( \Phi \). Sostanzialmente, l'effetto dell' applicazione di nabla ad un campo scalare genera un campo vettoriale (associato). Ma qual è il significato "fisico" di questo campo «gradiente»?
Per capirlo, consideriamo un caso unidimensionale; un campo le cui componenti lungo \( y \) e \( z \) sono nulle, mentre l'unica componente \( x \) è \( \neq 0 \). Un tale campo può essere ad esempio: \( (x^2, 0, 0) \). Applicando nabla otteniamo: \( \nabla(x^2, 0, 0) = \nabla_x + \nabla_y + \) \( \nabla_z = \frac{\partial x^2}{\partial x} = 2x \). la derivata lungo la direzione \( x \). La variazione del campo lungo \(x \).
E' abbastanza semplice capire ora nel caso generale il significato del gradiente. E' un vettore la cui direzione "punta" verso la massima variazione del campo scalare.
Si tratta di una generalizzazione del concetto di derivata per funzioni
di più variabili; infatti le componenti del gradiente sono le variazioni lungo gli assi, che sommate insieme, danno un contributo totale della variazione del campo nello spazio.
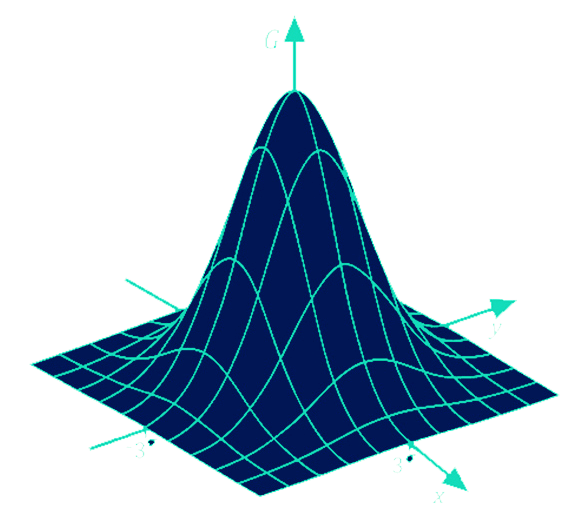
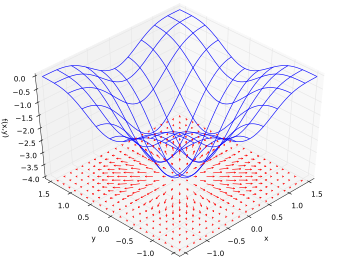
L'esempio più significativo è mostrato nella figura in basso: Il grafico (in blu) di una funzione di due varibili, rappresenta l'immagine del campo sul dominio. Il gradiente
(in rosso) è un vettore di due componenti (che vive nel piano). Osservate con attenzione come le frecce aumentano nelle zone del dominio che corrispondono sul grafico alla massima variazione, mentre
si riducono dove la variazione diminuisce. Seguendo la direzione del gradiente si va comunque nel verso crescente della funzione. Nel punto di minimo dove la variazione è nulla, il gradiente è \( 0 \).
Esistono diversi modi di indicare il vettore gradiente, quello più usato fa uso dell'operatore nabla ma esistono diverse notazioni altrettanto impiegate: $$ {\Large \nabla(\Phi) \hspace{7mm} \vec{\nabla}\Phi \hspace{7mm} grad(\Phi) \hspace{7mm} }$$
Interpretazione geometrica del gradiente
Il gradiente si presta ad una importantissima interpretazione geometrica, che verrà impiegata in diversi contesti. Consideriamo per semplicità (senza perdita di generalizzazione), un funzione \( F: {\mathbb R}^2 \rightarrow {\mathbb R} \) (il nostro campo scalare), definito sul piano \( {\mathbb R}^2 \). Diamo ora la definizione di curva di livello:
$$L_{c} = \{ (x, y) \in {\mathbb R}^2 | F(x, y) = c \} $$ Si tratta di un sotto-insieme del piano \( {\mathbb R}^2 \) tale che: per tutti i punti \( (x, y) \) appartenenti a questo insieme; la funzione assume un valore costante pari a \( c \). Questo insieme assume la forma di una curva del dominio della funzione \( F \) e come abbiamo detto si chiama curva di livello (c).
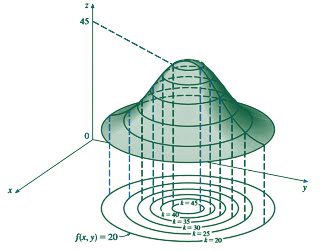
Se proviamo a calcolare la variazione infinitesima su una curva di livello, (il differenziale) ci accorgiamo di un fatto del tutto sorprendente!