Parlare di relatività è sempre entusiasmante! Non a caso in questo appuntamento entreremo un po nel vivo di una delle "due relatività" (quella più semplice, la relatività ristretta), che Einstein defini nell'annus mirabilis, il 1905 quando era un semplice impiegato dell'ufficio brevetti di Berna, alle prese con congegni meccanici vari da convalidare... un lavoro più da ingegnere che da fisico teorico...
$$ \diamond\diamond\diamond $$Una rivoluzione scientifica
Durante il tempo libero, Einstein lavorava intensamente alla sua vera passione, la fisica teorica, in particolare si dedicava ad alcune questioni di incompatibilità tra elettromagnetismo e meccanica. Più volte si era imbattuto in un problema apparentemente inutile (per molti) ma non per lui, il problema è il seguente: vi riporto un estratto del suo articolo pubblicato sugli Annalen Der Physics dad titolo: "Zur Electrodynamik bewegter Korper" tradotto: sull'elettrodinamica dei corpi in movimento, Einstein afferma:
Di che cosa sta parlando? Sta parlando dell'elettrodinamica di Faraday e di Maxwell. La teoria di Maxwell è una teoria classica, nel senso che vale anzitutto il principio di causalità ed il determinismo di Laplace. Si prenda ad esempio in considerazione l'azione elettrodinamica mutua tra due oggetti noti: un magnete e un anellino di rame. II fenomeno osservabile, in questo caso, dipende solo dal moto relativo dell'anello e del magnete, mentre l'usuale punto di vista traccia una distinzione netta tra i due casi in cui l'uno o l'altro di questi corpi è in movimento. In effetti, se il magnete è in moto e il conduttore è in quiete, nelle vicinanze del magnete sorge un campo elettrico con una certa energia definita, così da produrre una corrente là dove sono collocate delle parti del conduttore. Ma se il magnete è in quiete e il conduttore si muove, nessun campo elettrico sorge nei pressi del magnete. Nel conduttore troviamo tuttavia una forza elettromotrice per la quale non si ha alcuna energia corrispondente, ma che dà origine - assumendo l'uguaglianza del moto relativo nei due casi in discussione - a correnti elettriche con gli stessi percorsi e con la stessa intensità che si hanno a causa delle forze elettriche del caso precedente. Esempi di questo genere, uniti ai tentativi senza successo di scoprire un qualche moto della Terra rispetto al "mezzo luminifero" (l'etere, NdT), suggeriscono che i fenomeni dell'elettrodinamica e quelli della meccanica non possiedono alcuna proprietà corrispondente alla nozione di quiete assoluta.
Questo fatto per Einstein è una asimmetria che va assolutamente corretta per rendere la teoria priva di ambiguità intrinseche
$$ \diamond\diamond\diamond $$Il concetto di metrica di uno spazio
E' giunto il momento di entrare negli aspetti più tecnici della teoria, preparatevi... non si tratta di cose super-astratte, con un po di acume e pazienza vi assicuro che il tutto sarà "relativamente semplice".
In matematica, più precisamente in geometria, uno spazio metrico è un ente per il quale sia possibile determinare per ogni coppia di elementi la distanza tra essi. Più precisamente: se considero due punti dello spazio: \( a\) e \(b\), allora esiste sempre l'immagine di una funzione (detta distanza) definita come: $$ dist: (a, b) \rightarrow \mathbb R^{+} $$ L'unica richiesta è che la distanza sia simmetrica, definita positiva(o nulla se i punti coincidono) e triangolare per maggiori info ti rimando quì
$$ \diamond\diamond\diamond $$Metrica Euclidea
Per capire la struttura dello spazio-tempo voglio partire da qualcosa di già noto, qualcosa che conosciamo bene che il nostro cervello conosce in modo perfetto. A cosa mi riferisco? Sto parlando dello spazio in cui viviamo. Questo spazio, tra i matematici ha un nome ben preciso: si chiama spazio euclideo tridimensionale. Cosa centra Euclide? Il motivo è il seguente: in geometria tutto ciò che è "euclideo" è sostanzialmente "piatto", questo significa che vale il Teorema di Pitagora e la somma degli angoli di un triangolo è di \( 180° \equiv \pi \), in questo caso la metrica di questi spazi si chiama metrica euclidea ed è definita proprio dal teorema di pitagora. In \( n\) dimensioni si ha:
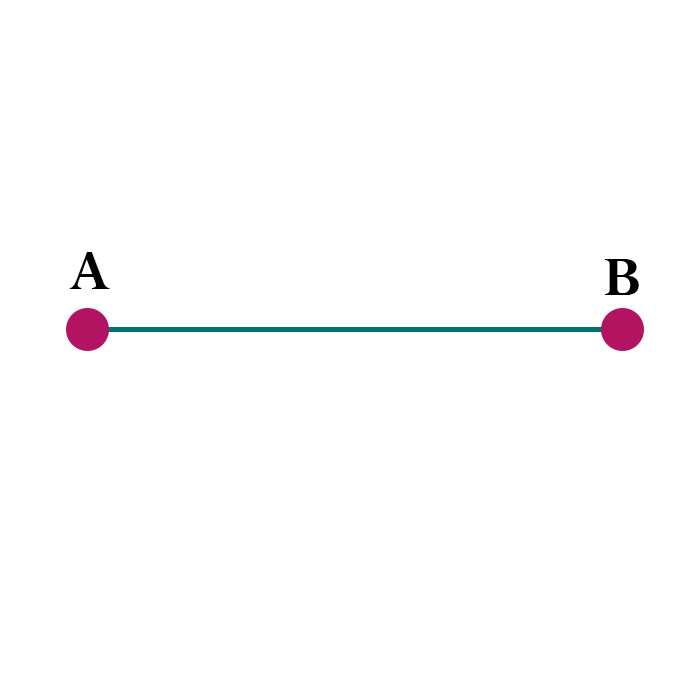
Distanza in \( \mathbb R \) $$ ||P-Q||_{R} = \sqrt{(x_i-y_i)^2} $$
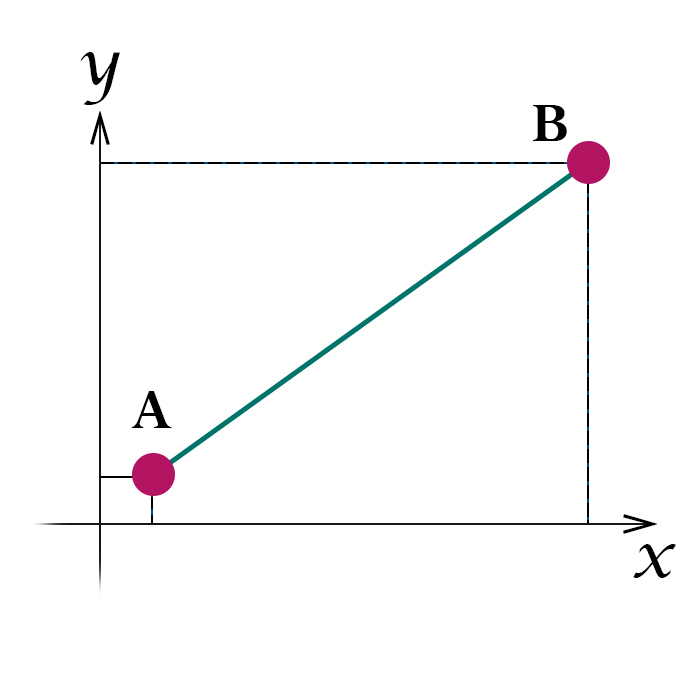
Distanza in \( \mathbb R^2 \) $$ ||P-Q||_{R^2} = \sqrt{\sum_{i=1}^2(x_i-y_i)^2} $$
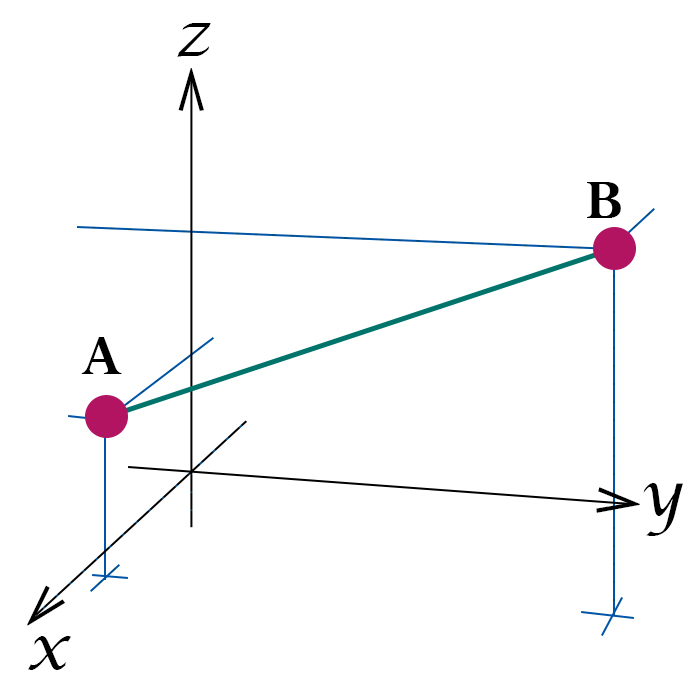
Distanza in \( \mathbb R^3 \) $$ ||P-Q||_{R^3} = \sqrt{\sum_{i=1}^3(x_i-y_i)^2} $$
Queste formule valgono negli spazi quando naturalmente su essi è stato definito un riferimento quindi una base vettoriale cui corrispondono le cosiddette coordinate, ossia dei numeri (con segno), che da un punto di vista geometrico, si ottengono mandando da un punto \( p\) le proiezioni ortogonali sugli assi coordinati del riferimento stesso. In tal modo scriviamo: $$ P \equiv \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \hspace{1cm} Q \equiv \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} $$ In questo modo, si spiega la formula della distanza. Se poniamo \( \Delta_i^2 = (x_i-y_i)^2 \) allora le formule assumono la seguente forma: \( dist(P, Q)_{\mathbb R} = \Delta_x^2 \), \( dist(P, Q)_{\mathbb R^2} = \Delta_x^2 + \Delta_y^2 \), \( dist(P, Q)_{\mathbb R^3} = \Delta_x^2 + \Delta_y^2 + \Delta_z^2 \). Più in generale vale la seguente formula. $$ \large \Delta_S^2 = \Delta_x^2 + \Delta_y^2 + \Delta_z^2 $$
$$ \diamond\diamond\diamond $$Metrica di Minkowski
Cosa succede se in uno spazio non vale più il teorema di Pitagora? Lo spazio non è più euclideo. Nessuno ci può garantire che la somma degli angoli in un triangolo sia \( 180° \), anzi non lo è affatto - inoltre la geometria è curva ed è piatta solo localmente... ma per ora non complichiamo le cose, "rimaniamo nel piatto", ma aggiungiamo un ingrediente speciale: "il tempo"
Dotiamo lo spazio euclideo tridimensionale di un orologio in ogni punto. In questo modo la la descrizione matematica di un punto passa da \( 3\) dimensioni a \( 4\) dimensioni; si parla quadrivettori o vettori a \( 4\) componenti, ottenuti semplicemente aggiungendo oltre alle \( 3\) dimensioni spaziali una quarta dimensione temporale \( t\) che rappresenta il tempo trascorso da un certo istante iniziale (l'origine dei tempi) di riferimento \( t_0\) $$ P \equiv \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \in \mathbb R^3 \longrightarrow \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ t \end{pmatrix} \in \mathbb R^4 $$
Chiamiamo con il nome di eventi questi punti a \( 4\) dimensioni. Un evento che si muove, varia sia spazialmente che temporalmente, anche se rimane fermo (esso varia nel tempo) - quando questi punti spostandosi, formano una traiettoria continua, essi formano una linea d'universo. Uno spazio simile non si può disegnare perchè non abbiamo dimensioni a sufficienza per graficarlo. Ora la domanda è: Qual è la metrica di questo spazio? Dello spazio tempo? La risposta ci viene niente di meno che dal professore di Einstein del Politecnico di Zurigo, Minkowski che riteneva Einstein fosse un nullafacente in matematica...(effettivamente non seguiva le sue lezioni di geometriariemanniana). La metrica dello spazio tempo si chiama Metrica di Minkowski
Consideriamo due punti dello spazio \( P \) e \( Q \). Per quanto gia detto, conosciamo o meglio, siamo in grado di calcolare la distanza \( \Delta s\) tra di essi attraverso la formula della metrica euclidea. Ora facciamo una cosa strana. Consideriamo il "metro di luce", ossia usiamo la luce per misurare, o come direbbero i fisici, per dare una definizione operativa di distanza. Un raggio di luce che parte dal punto \( P\) giungerà al punto \( Q\) dopo un certo istante di tempo \( \Delta t \) dato dalla formula della velocità: \( \small spazio = velocità \cdot tempo \)
Di queste due relazioni, consideriamo la seconda (a destra) ed eleviamo ambo i membri al quadrato. $$ \Delta s^2 = c^2\Delta t^2 $$
Portando tutto a sinistra dell'uguale ottteniamo: $$ \Delta s^2 - c^2\Delta t^2 = 0 $$ Sostituiamo ora l'espressione della distanza attraverso le coordinate ed invertiamo il segno: $$ c^2\Delta t^2 -\Delta_x^2 - \Delta_y^2 -\Delta_z^2 = 0 $$ Ebbene, questa espressione rappresenta una quantità che esprime quanto tempo impiega la luce a percorrere la distanza tra \( P\) e \( Q\) e mette in relazione le coordinate spaziali con il tempo e la velocita della luce. Possiamo perciò chiamare \( \Delta s \) questa quantita e quindi ottenere una pseudo-metrica euclidea della Metrica di Minkowski: $$ \Delta_s^2 = c^2\Delta t^2 -\Delta_x^2 - \Delta_y^2 -\Delta_z^2 $$
La caratteristica di questa metrica è che due eventi connessi da un raggio di luce sono hanno distanza nulla (pseudometrica).
$$ \diamond\diamond\diamond $$Trasformazioni di Lorentz
Consideriamo ora due eventi in due riferimenti \( \Gamma\) e \( \Gamma'\) uno di moto rettilineo-traslatorio ed uniforme rispetto all'altro di velocita relativa \(\mathrm V \) (tra i due). Nella foto è raffigurata la situazione:
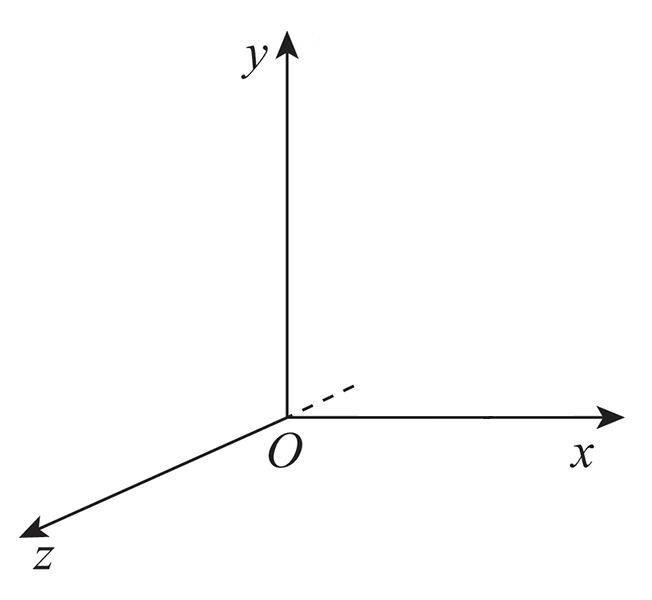
Sistema inerziale fisso
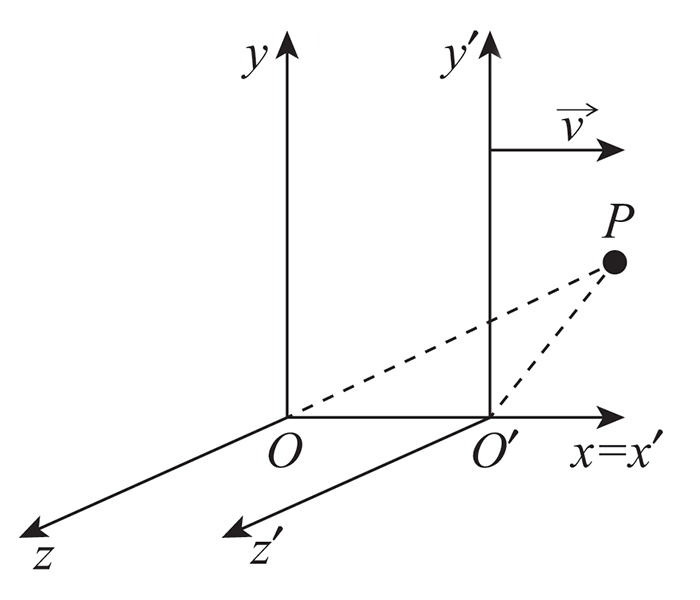
Sistema inerziale mobile
Siccome i due sistemi di riferimento sono l'uno di moto rettilineo ed uniforme rispetto all'altro e quello fisso è inerziale (anche quello mobile sarà inerziale); inoltre per il principio di relatività la distanza tra i due eventi vista dal sistema \( \Gamma\) deve essere uguale alla distanza dei due eventi vista dal sistema \( \Gamma'\) (per la covarianza delle leggi fisiche).
Esistono delle trasformazioni che verificano questa equazione, o meglio tali per cui questa equazione vale? Anzitutto cosa significa questa equazione? Quello che esprime è il fatto che la distanza è conservata (è invariante) da sistema a sistema. Ebbene queste trasformazioni esistono è si chiamano le Trasformazioni di Lorentz e ve le presento di seguito (per la felicità dei fisici :) )
$$ \large \Psi = \begin{cases}x=\frac{x'+Vt'}{\sqrt{1-\frac{V^2}{c^2}}} \\ y=y' \\ z=z' \\ t=\frac{t'+\frac{V}{c^2}x'}{\sqrt{1-\frac{V^2}{c^2}}} \end{cases} $$Da qui in poi il discorso si complica ulteriormente... per ora godetevi questo assaggio, presto ne vedremo delle belle ;)
Se ti interesa l'argomento, ho scritto un libro intitolato 8 viaggi nella scienza. Si parte dalla relatività, si passa per il mondo dell'informatica dei bit, si parla di quaternioni e numeri complessi, fino a giungere alla meccanica quantistica, in particolare al computer quantistico... e molto altro. Il testo è disponibile su Amazon, sia in formato ebook, che cartaceo.

